【從頭實作】感知機的原理以及實作

寫在前面

這篇文主要是希望更多人能夠跨越機器學習的高門檻所寫作的文章，初衷是希望更多人可以了解目前人工智慧最具有希望的一條分支-機器學習-類神經網路的原理，如果文章內容有幫助到你(妳)順手幫我分享一下，可以幫助更多人和這個神祕的領域相遇歐!

另外，如果有特別疑問的可以直接留言在底下或者直接FB找我!

什麼是「人工智慧｣

人工智慧簡單來說就是模擬人類的智慧的一種技術，就方法而言，是橫跨資訊、數學、心理、生物、等多個領域的一門有趣的科學。人類智慧的現象裡有一種最常見的能力「經驗學習｣也就是透過不斷的Try-Error來學會規則的方法，機器學習也就是透過數學的方法、並運用電腦程式來模擬「經驗學習｣。

感知機Perceptron

感知機的概念與數學模型最早於1943被心裡學家與數學家合作的一篇論文(A logical calculus of the ideas immanent in nervous activity)所提出，目的是希望能夠模擬類似神經元的傳遞資訊的機制，感知機就是一顆神經元的運作的模擬。一個感知機原則上可以表示成以下架構:

其中 x 是輸入信號，w 是感知機的權重，b是偏權值(也稱閥值)，net 是感知機的狀態，Y是感知機的輸出，d是期望的輸出值。

感知機的狀態數學的關係式可以表示成:

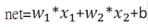
也就是:

感知機的狀態=加總所有的(輸入信號*對應權重)，直觀來說，一顆神經元的狀態取決於輸入信號的強度多寡與信號的重要性(權重)，不同種的輸入訊號有不同的重要性，而我們要決定的就是重要性的大小。

感知機的輸出的關係式可以表示成:

Y= Activation function(net)

Activation function 激活函數是一種非線性函數，用來將感知機的狀態值重新映射出去，在不同的類神經網路的架構裡有不同的激活函數，常見有sigmoid、ReLU等等

以Sigmoid函數為例子:

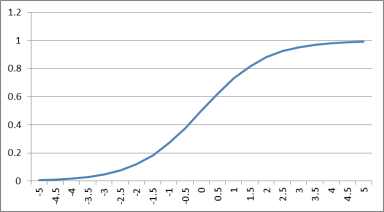
可以看得出來Sigmoid函數輸出介於0~1之間，輸入越大輸出越接近1，這種非線性的現象是在模擬神經元的傳導原則，當給予的刺激低於一定程度時，輸出電流趨近於0反之趨近於1。

用感知機來分類

感知機的行為大致上可以總結成:

1.輸入信號

2.信號加工(計算感知機狀態)

3.輸出信號

如果我們希望感知機能幫我們對一群數據做分類，我們可以利用輸出信號強弱來判斷，強(輸出值趨近於1)可以代表某樣本是某類別，弱(輸出值趨近於0)可以代表某樣本不是某類別。

感知機的失誤度量

為了衡量感知機輸出與期望輸出的失誤(loss)，我們用損失函數(loss function)來量化輸出預測與實際值的差異，最常見且本文使用的函數為: Square loss function 平方損失函數:

(目標輸出-實際輸出)^2

* loss function常見翻譯做「損失函數」，但我認為翻譯有歧義，應做「失誤函數」，loss function 的loss是指「失誤」，而非「損失」。

*Square loss function 通常會乘1/2方便取微分

感知機的學習

感知機的輸出信號取決於權重和閥值，因此我們希望透過經驗法則不斷的根據輸入以及期望輸出來修正權重和閥值，透過不斷重複迭代，讓輸出值逼近我們想要的輸出值。修正的方法通常利用梯度下降法來修正權重。

修正權重的量取決於損失函數對權重的偏微分，具體的細節可以參考我之間寫的另一篇文章: <Back Propagation with a Perceptron>。

具體而言的幾個實作感知機的重要公式:

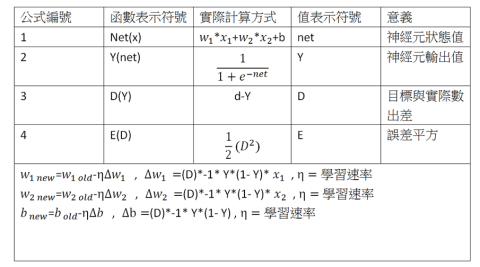
感知機的實作程式碼

public class Neural//神經元
{
   private double [] weight;//神經元權重組態
   private double bias;//神經元偏權組態
   public Neural(int dimension)//建構子 ,感知機的維度
   {
       weight=new double [dimension];
       bias=0;
   }
   public double []getWeight()
   {
       return weight;
   }
   public double getBias()
   {
       return bias;
   }
   private  double Net(double [] weight,double [] xi,double bias)//神經元狀態
   {
        double net=0;
        for(int i=0;i<xi.length;i++)
        {
          net+= xi[i]* weight[i];//加總(每個神經元權重*輸入)
        }
        net+=bias;//最後加篇權值
        return net;
   }
   private  double Y (double net)//神經元輸出
   {
       return Sigmoid(net) ;
   }
   private   double Sigmoid(double x) //Sigmoid函數
   {
        return (1/( 1 + Math.pow(Math.E,(-1*x))));
   }
   private double D(double d,double Y)//誤差
   {
       return d-Y;
   }
   private  double E(double D)//平方誤差
   {
       double E=0.5*D*D;
       return E;
   }  
 
   public  double Iterate(double [] xi,double d,double learningRate)//一次迭代 ,輸入,期望輸出 回傳本次迭代誤差函數輸出
   {
       //---前向傳遞
       double net=Net( weight,xi,bias);
       //System.out.println("net"+net);
       double Y=Y(net);
       //---
 
       //---誤差計算
       double D=D(d,Y);
       //---
 
       //---平方誤差(誤差函數)
       double E=E(D);
       //System.out.println(E);
       //---
 
       ////誤差倒傳遞
 
       //---對每個weight做更新
       for(int i=0;i<weight.length;i++)
       {
            double deltaWeight=D*-1*Y*(1-Y)*xi[i];//weight 修正量
            weight[i]= weight[i]-learningRate*deltaWeight;//更新
       }
       //---
 
       //---對bias做更新
       double deltaBias=D*Y*(1-Y)*-1;//bias 修正量
       bias=bias-learningRate*deltaBias;//更新
       //---
 
       ////---
       return E;
   }
 
}

完整的專案網址：https://github.com/whuang022ai/PerceptronGUI

感知機訓練數據

感知機訓練可以使用Anderson’s Iris data set鳶尾花數據集，這個數據集是統計學、機器學習常使用的一數據集，我這裡有一份把setosa種類標記為1，versicolor標記為0的數據，總共一百筆資料。利用這個數據來進行感知機的分類訓練。可以在這邊下載!

感知機誤差降低的過程

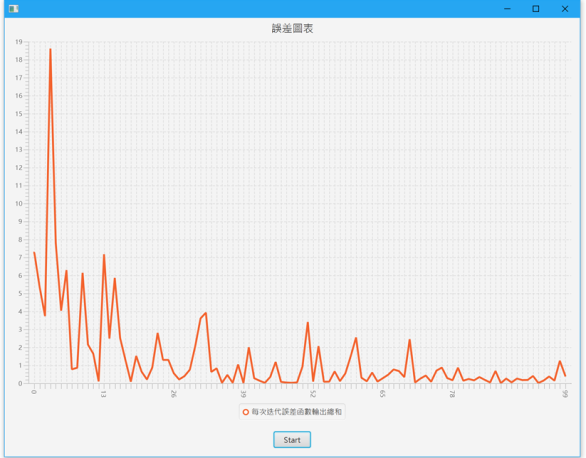
以上的圖表是經過100次迭代產生的誤差圖表，橫軸是迭代的第x次，縱軸則是該次的誤差函數輸出總和，可以發現梯度下降法的誤差逐漸降低，也就是輸出逐漸逼近我們想要的值，當低於一定程度時，我們成為收斂，也就是感知機已經透過經驗學習到什麼樣的輸入模式該給出什麼樣的輸出。

結語

類神經網路是非常靈活自由的一種技術，從激活函數、誤差函數以及網路的連結架構(例如 多層感知機)、層數、神經元單元的變化(例如LSTM)，基本上可以隨意搭配，只要能有效解決問題即可。而梯度下降法的更新法則會因為不同的網路結構而改變，因此如果想要實做自己的類神經網路，是有必要熟悉偏微分以及鏈鎖律，才能推算出權重的更新規則。